Сечет как русский котангенс в Египте
Секед или сечет угла. Теперь, после необходимых пояснений, мы приблизились к смыслу данной статьи - к исследованию понятия «секед». В книге «Математика времен фараонов» Ричард Гиллингс объясняет: «Секед правильной пирамиды - это наклон любой из четырёх треугольных граней к плоскости основания, изменяемый энным числом горизонтальных единиц на одну вертикальную единицу подъёма. Таким образом, эта единица эквивалентна нашему котангенсу угла наклона. В целом, секед пирамиды - это своего рода дробь, выраженная в стольких-то ладонях (единицах измерения) горизонтально на каждый локоть вертикального подъёма, где 7 ладоней равны одному локтю. Египетское слово секед таким образом родственно нашему современному слову ГРАДИЕНТ» (ФАР, с. 110). Уточню, что родственно не по словообразованию, а по значению. А вот прежде, чем искать русский эквивалент данного слова, хотел бы привести его геометрическое пояснение, рис. 3.

Рис. 3. Понятие секеда по Р. Гиллингсу
Данная иллюстрация взята из (ФАР, с. 110, рис. 28). «Понимание этой простой системы стало ключевым моментом в определении техники съёмки древних бриттов в Марлборо-Даунс» (ФАР, с. 110). Замечу, как постепенно «предки британцев» (хотя на самом деле не предки, а предшественники) у него превратились в «древних бриттов» (то есть уже и не предков, а подлинных кельтов, и даже не скоттов и не пиктов, а именно бриттов). Вот пример информационной британизации неолитической истории, который происходит не в отдалённое время, а на наших глазах, и не академической археологией, а альтернативной, пока еще не признанной!
И далее даётся пример: «Благодаря пониманию метода древних египтян, стало ясно, откуда взялись «странные» углы склона вроде 51051', как в Великой пирамиде. Он является производным от простого числового отношения высоты и основания пирамиды, которое в случае Великой пирамиды равно 7:11. Это справедливо для всех пирамид. Но упоминание этого простого факта я не нашел ни в одной книге, прочитанной по этой тематике. Числовой ключ к пирамидам заключен в отношении их высоты к основанию» (ФАР, с. 100-111). - Фарлонг ошибается: секед пирамиды будет 11:7, а не 7:11. Он попутал тангенс с котангенсом. Впрочем, это весьма распространенная для нематематиков ошибка. Ибо нам было бы естественным измерять горизонталь в вертикалях, а не наоборот.
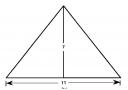
Рис. 4. Отношение основания к высоте в Великой пирамиде
Ту же ошибку он делает, подписывая рис. 4 «Отношение высоты к основанию Великой пирамиды» (ФАР, с. 99, рис. 22). Но для меня важно не это, а то, что, процитировав работу Р. Гиллингса, он помог нам не только понять термин, но и узнать его название на языке египтян. А далее мы уже будем делать собственные выводы.
Слово «сЕкед» при переносе ударения назад удивительно совпадает с русским словом «секёт» (как в смысле «рассекает», так и в сленговом значении «понимает»). А поскольку в Египте вначале господствовала русская культура, не будет большим преувеличением предположение о том, что египетское слово образовалось из русского. Более того, русский глагол «сечь» имеет форму СЕКУ, которая содержит звук К. Что же касается последнего согласного звука Д, то он, как можно понять, является просто озвончённым звуком Т. Более того, можно наметить словообразовательную модель, по которой из глагола возникает соответствующее существительное, например, кричИт-крЕчет, сечЁт-сЕчет. Иными словами, слово СЕЧЕТ поначалу, возможно, означало СЕКУЩУЮ линию, весьма востребованное в нынешней геометрии слово.
В том, что это слово означало СЕЧЕНИЕ, видно на рис. 4. Вертикаль СЕЧЁТ горизонталь пополам, отсекая от нее отрезки по 5,5 единиц измерения. Таким образом, слово СЕЧЕТ оказывается русским не только по словообразованию и фонетике, но и по своему исходному смыслу.
Однако я хотел бы пойти существенно дальше. В средние века на Западе возникает математическая наука тригонометрия. Вот что говорит Википедия об истории этой науки:
«Истоки тригонометрии берут начало в древнем Египте, Вавилонии и долине Инда более 3000 лет назад. Индийские математики были первопроходцами в применении алгебры и тригонометрии к астрономическим вычислениям. Лагадха (450-350 до Р.Х.) - единственный из самых древних известный сегодня математик, использовавший геометрию и тригонометрию в своей книге «Джьётиша-веданга» («Jyotisa Vedanga»), бо́льшая часть работ которого была уничтожена иностранными захватчиками.
В Европе основы геометрии закладывал древнегреческий астроном и математик Аристарх Самосский (310-230 до Р.Х.) в труде "О величинах и взаимных расстояниях Солнца и Луны". Греческий математик Клавдий Птолемей (87-165 от Р.Х.) также внёс большой вклад в развитие тригонометрии». Заметим, что это - история задач, но не история названий.
Там же можно прочитать и об истории названий: «Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива»), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.Современное обозначение синуса sin и косинуса cos введено Леонардом Эйлером в XVIII веке. Термины «тангенс» (от лат. tangens - касающийся) и «секанс» (лат. secans - секущий) были введены датским математиком Томасом Финке (1561-1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583) .Сам термин тригонометрические функции введён Клюгелем в 1770».
Итак, несколько переводов, выбрасывания гласных, переосмыслений - и от русского слова, и даже от русского представления ничего не осталось. Сейчас в школе сначала изучается синус, потом косинус, потом отношение между ними - тангенс, а затем величина, обратная тангенсу - котангенс. Всё внимание математиков сосредоточено на синусе как на основной величине тригонометрии, тогда как котангенс - очень далёкое, периферийное понятие.
Заметим, что русское понимание было существенно иным: на первом месте стоял котангенс как исходная величина, причём не тригонометрии как науки о ТРЕУГОЛЬНИКАХ, а иной науки. Какой? Об этом стоит поразмышлять, анализируя дальнейшие исследования Фарлонга.

Рис. 5. Соположение планов трёх пирамид Гизы
Вписанные квадраты. На рис. 5 (ФАР, с. 105, рис. 25) мы видим изображения трёх пирамид в плане, наложенные друг на друга. На рисунке имеется пояснение: «Одна сторона основания пирамиды Хафры равна 15/16 соответствующего размера Великой пирамиды. Одна сторона пирамиды Менкаура чуть больше половины стороны пирамиды Хафры». Итак, соотношение между сторонами трёх пирамид составляет целые числа, или, как сказали бы представители ядерной физики, квантованы. Это - один из многочисленных примеров того, что горизонтальные размеры всех пирамид имели одинаковый масштаб, и, если выражать всё в целых числах, имели соотношение 15:30:32. Таким образом, первичными были не углы треугольника, как в тригонометрии, а отношения между катетами. Но и не между катетами, а между длиной и высотой. А это предполагает даже не пирамиду, а призму, а на плоскости - прямоугольник и любую иную фигуру, имеющую не более 2 вершин, в частности - 1. Что же касается треугольника, то и он может быть измерен собственной высотой, которая должна быть вертикалью, опущенной из вершины. Но прямые линии этих склонов значения не имеют, они могут быть и не прямыми, а ломаными или кривыми. Так что предлагается в качестве эталонной фигуры не треугольник, я любая плоская фигура, чьи параметры можно задать длиной и высотой. Разумеется, наиболее совершенной из них будет равнобедренный треугольник.
Итак, насколько можно видеть, для совершенных фигур выделяются ДЛИНА и ВЫСОТА, которая тут называется СЕЧЕНИЕМ или, еще точнее, СЕЧЕТОМ. И как пропорции одной пирамиды, так и соотношения между пропорциями разных пирамид, выражаются целыми числами, причем не от меньшего к большему, а от большего к меньшему. Иными словами, пропорции большой пирамиды должны быть записаны как числа 11:7, а между пирамидами Гизы - как числа 32:30:15. Заметим, что числа последнего соотношения могут быть записаны как 2×4×4:2×3×5:3×5. Иными словами, числа эти тщательно подобраны. Таково ИЗМЕРЕНИЕ СЕЧЕНИЙ или СЕЧЕТОМЕРИЕ.
Возникает впечатление, что из слова СЕЧЕТ позже за счет передвижения ударения на последний слог и редукции первого гласного звука возникло слово СЧЁТ, а от него - производный глагол СЧИТАТЬ. Иными словами, СЧИТАТЬ, это вовсе не воспроизводить репертуар числительных (то есть, не произносить ОДИН, ДВА, ТРИ...), а составлять пропорции типа 11:7 (оба числа - простые), 13:11, 17:13, 19:17 для высот пирамид или составлять соотношения типа 81:64, 64:60, 32:27 и т.д. для их размеров. Так что СЧЕТОМЕРИЕ постепенно становится просто СЧЕТОМ или РАСЧЁТОМ.
Такова реконструкция слова СЧЁТ по реликту, сохранившемуся в египетском языке. Замечу также, что в словаре Фасмера слова СЧЁТ и СЧИТАТЬ отсутствуют.
Написать отзыв
Вы должны быть зарегистрированны ввойти чтобы иметь возможность комментировать.